If you’re a sci-fi fan, you’ve probably seen these in movies. And I’m guessing you’ve heard a lot about them in pop culture. The problem is, pop culture and movies don’t do a very good job of describing black holes.

First off, let me clear up a common misconception: Black holes do not act like giant space vacuum cleaners, sucking in everything around them. Describing them as “gobbling up” anything is inaccurate.

The representation in movies that bugs me the most is in J.J. Abrams’ Star Trek reboot, when the bad guy falls into a black hole and the good guys almost get pulled in with him. First of all, please…black holes do not growl. And basically none of what happens in that scene is accurate.

So…what are black holes, really?

The first concept we need to grasp in order to understand black holes is escape velocity.

I touched on escape velocity back in my post on how orbits work. It’s simply the speed and direction you need to escape the gravitational pull of any given object.

The diagram above shows the different orbits any object can have around a celestial body—in this case, the Earth. The circle and two ellipses all take the object back to its starting point. The parabola and hyperbola, however, take the object away from the influence of Earth’s gravity…into space.

Escape velocity depends on only two things: the mass of the celestial body and the distance between the center of mass of the system and the escaping object.

(By the way, the center of mass can be thought of as like the fulcrum of a teeter-totter: If you want the teeter-totter to stay balanced, but one side is perhaps a bit heavier than the other, where do you put the fulcrum? It’s always found closer to the heavier or more massive side of the system.)

So…back to escape velocity. As you might expect, black holes have a high escape velocity—that is, an object would need to move extremely fast in order to escape one. But it’s a bit more complicated than that…

Let’s start by taking a look at the anatomy of a black hole.

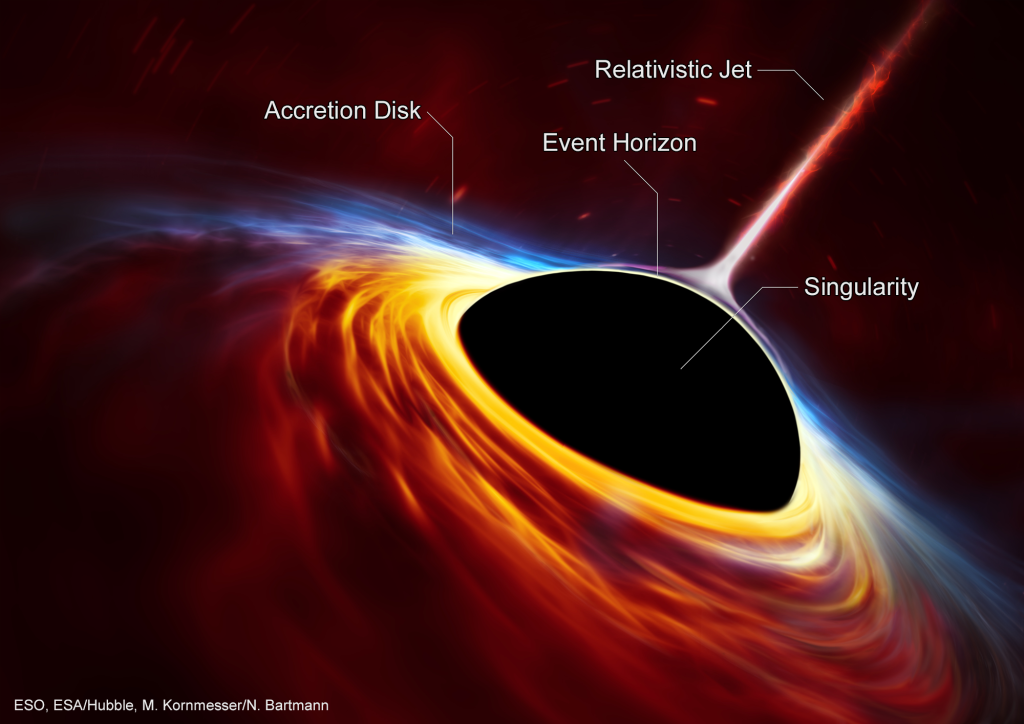
At the heart of every black hole is a singularity—a place in time and space that has zero radius, but infinite density.

I know. Whenever I try to imagine that, my brain just kind of goes…whaaaaa?

Trying to actually conceptualize a point that has absolutely zero radius/diameter and yet is filled with so much stuff that it’s infinitely dense is kind of brain-breaking. Instead, let’s explore how an object gets to be a singularity in the first place.

We start with the collapse of a star’s core. We’ve already explored two other types of compact objects, besides black holes—white dwarfs and neutron stars. Both of these objects result when the collapsing core is too massive for “conventional” physics to support them. They must rely on the material strength of degenerate matter.

If the collapsing core contains more than 3 M_☉ (solar masses) of star stuff, however…no force in the universe can stop it. There is no material strength that can support an object 3 times the mass of our sun that is not engaging in nuclear fusion. Such an object can’t have any size greater than zero because the stuff it’s made of would have more room to collapse.

It still has 3 M_☉ of stuff, though, and that much stuff in a space of zero radius means infinite density.

Now, note the event horizon in the illustration above. What the heck is that?

It’s a sphere—in two dimensions, a circle—around the singularity, its size determined by the Schwarzschild radius (shown here as R_Sch).

The Schwarzschild radius is the distance from the singularity that any object has to be in order to escape the singularity’s gravity. But why?

Because here’s the key: the escape velocity of a singularity is greater than the speed of light.

As many of you may know, the speed of light is what we tend to call the “universal speed limit.” And in space, the only police are the laws of relativity themselves. It’s physically impossible to break the universal law that you can’t travel faster than the speed of light. Why? I’m honestly not sure.

The point is, if the escape velocity of a singularity is greater than the speed of light, then nothing can ever escape it.

…as long as we’re talking about stuff within the event horizon. Outside the event horizon…you are safe.

Well, as long as you’re traveling fast enough. But at least the escape velocity is actually physically possible to achieve.

In fact, if the sun were magically, instantaneously replaced by a black hole of the exact same mass, none of the orbits in the solar system would change—because none of them are inside the Schwarzschild radius an object of the sun’s mass would have if it were a black hole.

So, what does the gravitational field around a black hole look like, anyway?

Notice how, at the “surface,” so to speak, of these diagrams, gravity is pretty similar between a star like the sun, a neutron star, and a black hole. It’s only when you get super close to the object that you start to notice enormous forces acting on you.

We actually see this effect with our own sun. Generally, Isaac Newton’s physics equations are sufficient to describe planetary orbits. When you get super close to an object, though—even one as small as our sun—you need more advanced equations. Mercury’s orbit, in fact, is close enough that subtle changes (called the advance of perihelion) can only be explained by Einstein’s equations.

Likewise, from a distance, black holes might as well be just another star. Get too close, though, and you don’t just need Einstein’s physics—you need mathematics from more recent greats like Stephen Hawking. And that’s before you even reach the event horizon.

So…what’s with the “accretion disk” we see up in that labeled illustration I showed you of a black hole?

Accretion disks are a feature of black holes unique to those in binary systems—that is, those that have a companion star.

And, yes, black holes can have companion stars. Their Schwarzschild radius depends only on their mass, and doesn’t even extend to where their surface had been before they collapsed. A black hole the mass of the sun would have a Schwarzschild radius of only 3 km, which is a tiny fraction of its present radius. The event horizon of most black holes would be mere kilometers from the singularity—not a meaningful distance in astronomical terms.

Anyway, a great deal of binary systems engage in mass transfer, literally the transfer of mass from one star to the other. In a system involving a compact object (white dwarf, neutron star, or black hole), this transfer would only go one way—from the star to the compact object.

But transferred mass can’t just fall directly onto a compact object. It’s too tiny for that. Think of the mass transfer system as being like water draining from a bathtub. The drain isn’t very big compared to the bathtub. Now, all liquids have at least some angular momentum—that is, circular currents. This momentum has to be conserved as the water pours down the drain. That means the current has to speed up. The result is a mini-whirlpool that I’m sure you’ve observed before.

The same thing happens with binary systems, especially those involving compact objects. Squeezing the mass from a giant star into the radius of a white dwarf (roughly that of the Earth) or a neutron star (smaller than Los Angeles) means creating a giant space whirlpool of matter that gradually falls onto the object.

In the case of a black hole, an object of zero size, an accretion disk is a given.

Alright, so we’ve covered singularities, event horizons, and accretion disks. What the heck is the relativistic jet you see above?

That’s a discussion for another day—as is what it would actually be like to fall into a black hole! (And by the way, it’s pretty much nothing like the movies. Except maybe Interstellar. That one comes pretty close.)