When you look up into the sky on a clear night away from the glare of the city, you see trillions upon trillions of stars.

Thousands of years ago, the classical astronomers saw the same thing you do today—except perhaps a little different, due to the ever-changing cosmos. And, like you, they weren’t satisfied with just looking. They wanted to know what was out there.

For hundreds of years, they developed model after model to explain why the stars seemed to orbit the Earth and why certain objects in the sky—which they named planets—seemed to wander backwards from time to time.

Tycho Brahe, an astronomer known mainly for what he got wrong, dismissed the idea of the Earth orbiting the sun because he could detect no parallax between the stars.

If he had been able to measure parallax, he might have realized that the universe was much larger than any of his fellow classical astronomers imagined.

So what is parallax…and how can it help us measure the distances between stars?

Before we dive into parallax, let’s simplify this whole discussion. I’m about to tell you about a method of measuring distance in space that isn’t all that different from measuring the distance across a river on Earth.

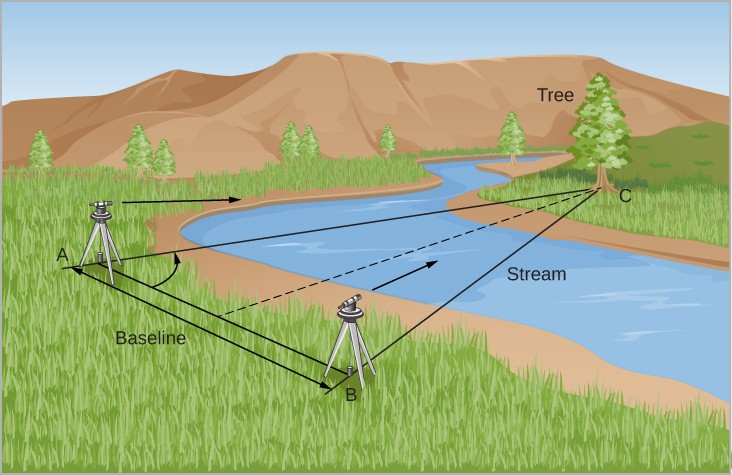
Let’s say you want to know how far away a particular tree is, but you can’t just walk over with a tape measure—there’s a current of water in the way.

So you set up two instruments a distance apart from one another on your side of the river. You measure exactly how far apart your instruments are, and that distance serves as your baseline.

Then you use those instruments to measure the angle formed between the baseline and the tree across the river.

Take a moment to understand what we’re doing. Basic geometry tells us that if we know three things about a triangle—as long we know at least one side—we can find all the sides and angles in that triangle.

And what triangle are we talking about? Well, we’ve got three corners—the two instruments and the tree. The distances between each of them make up the three sides.

So…we know the length of our baseline. If we know the angle between each of the other sides and the baseline, then we know three things. And we can calculate the distance to the tree.

The same thing works in space.

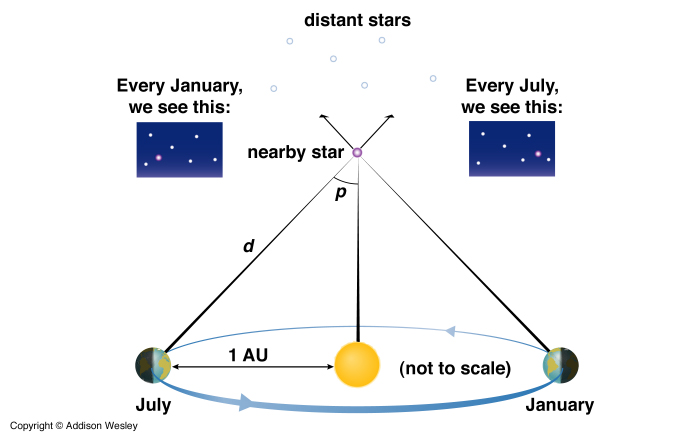
The stars are so far away that we need a much larger baseline to get an accurate measurement on any of the angles. So we use the diameter of Earth’s orbit.

Okay…but we’re not some omniscient being, hovering over Earth and able to measure that diameter. How the heck can we find out our baseline?

Well, lucky for us, we already know that Earth’s average distance from the sun is 93 million miles—or 1 AU (astronomical unit). So the diameter of Earth’s orbit is 2 AU.

Now we just need to measure the parallax of the stars.

Oh, hey, there’s that parallax term again.

So what exactly is parallax?

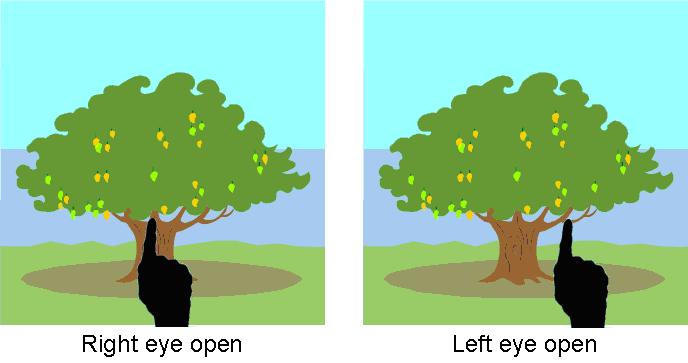
It’s just a fancy word for the apparent change of position of an object when the observer changes position.

Okay…that’s a kind of technical definition. How about in plain English?

Your two eyes aren’t in the same place on your face. So they have slightly different perspectives. Think of them as two different observers. When you change which eye is open, you change the observer’s position.

Any object fairly close to you—in the case of this diagram, your finger—will appear to change position against its background.

The same goes for the stars. And when the change in the observer’s position (Earth’s position) is the diameter of its orbit, we can detect parallax among closer stars against the background of more distant stars.

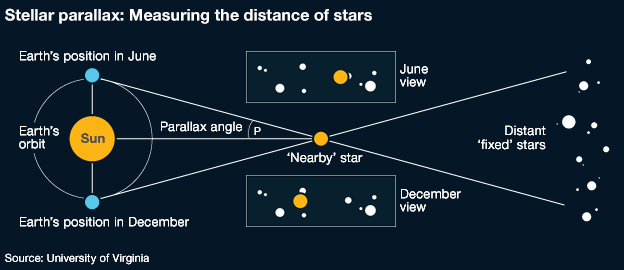
See how this image refers to parallax as an angle? Parallax is useless to us unless we can calculate it, and it’s calculated as an angle. More specifically, it’s the angle between our line of site to the nearby star, and the sun’s line of sight to the nearby star.

Don’t worry about how the heck we can calculate the sun’s line of sight when we can’t set foot on our sun. We can calculate the parallax angle just from examining images taken when Earth is at each of these positions in its orbit—in this case, June and December.

If we calculate the parallax angle in June and then again in December, we can easily calculate the angles between the triangle’s sides and baseline—it’s simple geometry. And from there, we can calculate the distance to the star.

As it turns out, even the famous light-year (ly) is too small for use in these calculations. Astronomers have come up with a special unit that’s 3.26 ly long—the parsec (pc).

Wait a second…how long is a light-year, again?

It’s the distance light travels in one year. If you thought light travels instantaneously…well, you’re mistaken. But it appears to. If it can go that fast, imagine how far it would go if we gave it a whole year to travel?

Yeah…that’s a lot of distance.

So…how far away would you guess the closest star to be?

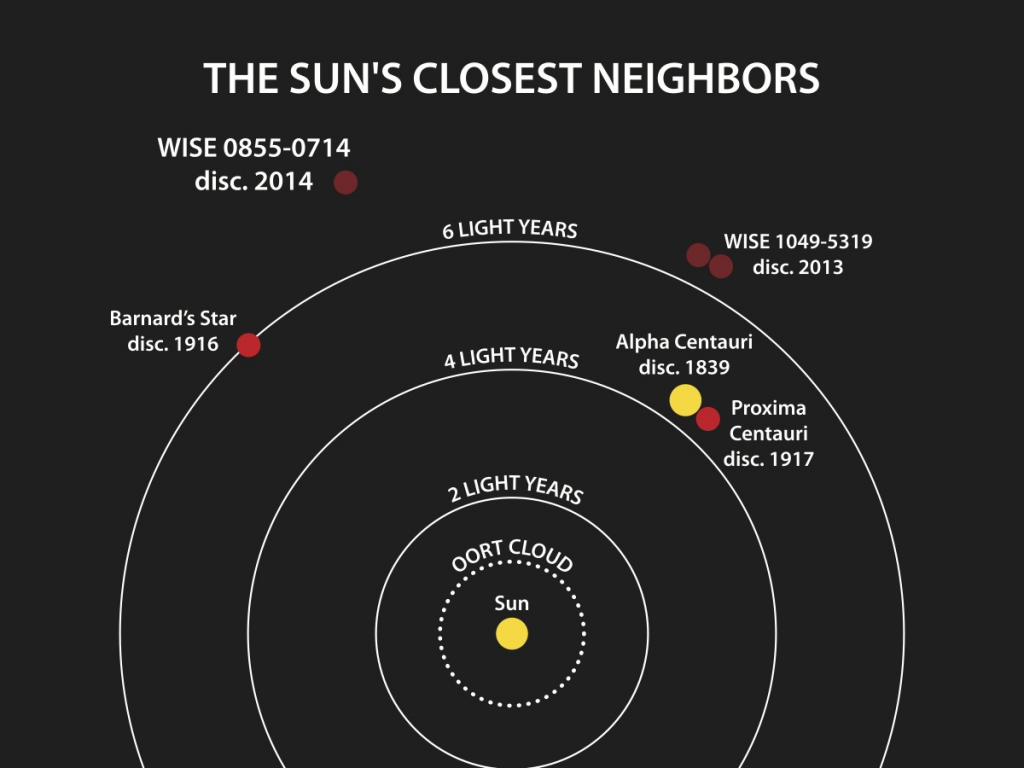
Here’s a few of the sun’s closest neighbors.

Our closest interstellar neighbor is the Centauri system, a star system with three stars orbiting one another. Since they’re orbiting at snail pace, one of its stars is named Proxima Centauri for its seemingly perpetual proximity to us.

Proxima Centauri is 4.2 ly away. That’s 1.2877 parsecs.

But what does that even mean? I mean, are all stars 1.2877 parsecs apart from one another?

Well, not exactly. There are variations. Some are closer; some are farther. Sirius, the brightest star in the sky, is a whole 2.64 parsecs away from us. And believe me, that’s far. It’s 8.61 ly away.

There’s only one problem with stellar parallax as a tool to measure distance. We need to get accurate images of the stars to measure accurate parallax. And the atmosphere likes to get in our way.

That’s what the European GAIA mission was for, back in 2013.

Over the course of about 6 months, it was able to measure the parallax of a billion stars to a 10% degree of uncertainty—not too bad when we’ve got the whole universe to measure, and only a 2 AU baseline to work with.

GAIA isn’t the only satellite to measure stellar parallax. The European Space Agency also launched the Hipparcos satellite back in 1989, and it returned two extensive catalogs of stellar parallax measurements over the course of four years.

How extensive, you ask? Well, one of them contained 120,000 stars with parallaxes 20 times more accurate than ground-based measurements, and the other contained over a million that were just as accurate as ground-based measurements.

NASA’s Space Interferometry Mission was planned to launch in 2009 and get us even better results, but it was cancelled in 2010.

Parallax is just one way to measure the distances to the stars. Next up, I’ll talk about proper motion.